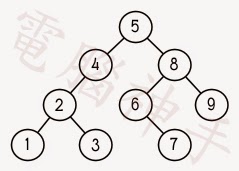
二元搜索樹是一種二元樹,給定某個排序函數,比如 < ,每個元素的左子樹都 < 該元素,而該元素 < 其右子樹。圖 下展示了根據 < 排序的二元樹。
樹(Tree)是由一些有連結的節點(node)組成,且架構如下:
1.有一個特別的節點叫做根節點(root)
2.除了root以外剩下的節點被分成
個相互獨立的點集合,每一個集合都構成樹。我們稱這些樹為根節點的子樹(node subtree),每個子樹的根節點被稱為子節點(Child)。
換個方法定義,樹(Tree)是一個連通的圖(graph),兩點之間恰有一條路徑可達。此外,一個節點的度數(degree)就是這個節點的子節點個數。整棵樹的度數N也就定義為所有節點度數的最大值,此時定義這棵樹是個N元樹。森林(Forest)是許多樹的聯集。
樹的表示式
除了把Tree圖畫出來以外(這樣太佔空間了),我們可以用一個List列出來。如由上方的圖我們可以用括弧表示每個子樹,因此整棵樹列出來像這樣:
(1 (2 (4 (5, 6(7))), 3))
每一個node可以表示成如下:
data link
1 link 2 … link
但是這樣會有浪費記憶體的可能,所以我們考慮用另一種表示方法,讓這棵樹或是森林轉換成二元樹。這樣每個node只要記錄最多兩個link就好了。在此之前我們先介紹最重要的樹狀結構:二元樹(Binary Trees)。
二元樹的每個節點至多有兩個子節點,且有分左右。下面以一個節點的結構可表示如下:
然後用C#呈現的範例:
1.先定義節點物件
public class BinaryTreeNode
{
public BinaryTreeNode Left { get; set; }
public BinaryTreeNode Right { get; set; }
public int Data { get; set; }
public BinaryTreeNode(int data)
{
this.Data = data;
}
}
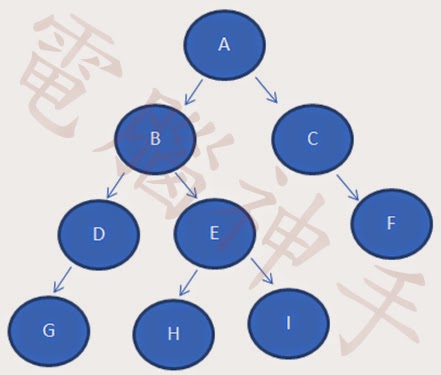
2.使用節點物件來建立二元樹
BinaryTreeNode nodeRoot = new BinaryTreeNode("A")
{
Left = new BinaryTreeNode("B")
{
Left = new BinaryTreeNode("D")
{
Left = new BinaryTreeNode("G"),
Right = null
},
Right = new BinaryTreeNode("E")
{
Left = new BinaryTreeNode("H"),
Right = new BinaryTreeNode("I")
}
},
Right = new BinaryTreeNode("C")
{
Left = null,
Right = new BinaryTreeNode("F")
}
};
3.前序訪問
Action<string> printValue = delegate(string v)
{
Console.Write(v + " ");
};
PreOrderTraversal(printValue, nodeRoot);
public static void PreOrderTraversal(Action<string> action, BinaryTreeNode root)
{
if (root == null) return;
action(root.Data);
PreOrderTraversal(action, root.Left);
PreOrderTraversal(action, root.Right);
}
4.中序訪問
Action<string> printValue = delegate(string v)
{
Console.Write(v + " ");
};
InOrderTraversal(printValue, nodeRoot);
public static void InOrderTraversal(Action<string> action, BinaryTreeNode root)
{
if (root == null) return;
InOrderTraversal(action, root.Left);
action(root.Data);
InOrderTraversal(action, root.Right);
}
5.後序訪問
Action<string> printValue = delegate(string v)
{
Console.Write(v + " ");
};
PostOrderTraversal(printValue, nodeRoot);
public static void PostOrderTraversal(Action<string> action, BinaryTreeNode root)
{
if (root == null) return;
PostOrderTraversal(action, root.Left);
PostOrderTraversal(action, root.Right);
action(root.Data);
}
二元樹的走訪
因為要直接表示一棵二元樹有些困難,所以我們以某些特定順序探訪這棵樹,所得的序列就是這棵樹的資料。
前序表示法preorder:root, left-subtree, right-subtree
中序表示法inorder:left-subtree,
root, right-subtree
後序表示法postorder:left-subtree, right-subtree, root
【題2】給定二元樹的preorder以及postorder,求inorder。
將一般的Tree或Forest化簡為Binary Tree,有一種常用的方法Left-Child-Right-Sibling:也就是將所有節點重新定義,其左子節點仍為此節點的左子節點,右子節點定義為這個節點的右邊兄弟。
二元搜尋樹(Binary Search Tree)
Binary Search Tree(BST)是一個二進制樹(最多每節點2兒童的)與每一個節點Key和相關聯的值。還一個BST具有為每個節點,左子樹僅包含具有較小(或相等)的關鍵節點和右子樹包含有嚴格較大密鑰僅節點的屬性。此屬性將讓我們在時間成正比,樹高進行插入和刪除操作。後來更多的時間複雜度。\
對於陣列來說,要查找一筆資料用二分搜尋法可以在 時間內達成,但是如果現在的資料結構不是陣列呢?假設這些資料分散在記憶體中,那麼只要建立二元搜尋樹(BST)的結構,平均只要 的時間就可以新增、查找資料。BST是一個二元樹,並滿足以下條件:對於任意節點S,S的左子樹的所有節點的鍵值不大於S的鍵值,S的右子樹的所有節點的鍵值不小於S的鍵值。
堆積heap
堆積是一種二元樹。其最大的特點為每個節點的鍵值永遠比左子節點或右子節點上的鍵值小(或大)。這樣可每次以 取得最小值(或最大值),然後用 的時間整理heap,對於動態資料的處理相當方便。
該BST類被聲明如下:
public class BinarySearchTree<Tkey, Tvalue> where Tkey : IComparable<Tkey>
在BST的節點可以由任何類型實現IComparable被鍵入。對所用的值的類型沒有限制。簡單的節點定義範例:
protected class BinaryKeyValueNode<Tkey, Tvalue> where Tkey : IComparable<Tkey>
{
public Tkey Key { get; set; }
public Tvalue Value { get; set; }
public BinaryKeyValueNode<Tkey, Tvalue> Parent { get; set; }
public BinaryKeyValueNode<Tkey, Tvalue> LeftChild { get; set; }
public BinaryKeyValueNode<Tkey, Tvalue> RightChild { get; set; }
public BinaryKeyValueNode(Tkey key, Tvalue value)
{
Value = value;
Key = key;
}
}
所以,每個節點由一個鍵和一個值,並保持一個參考子樹均(子節點)和其父。這些字段和建構的BST:
private Random random;
protected BinaryKeyValueNode<Tkey,
Tvalue> Root { get; set; }
public int Count { get; protected set; }
public BinarySearchTree()
{
Root = null;
random = new Random(1);
Count = 0;
}
我們維持計數(可選)和參考根節點(最初為null)。
插入的內容如下:
public void Insert(Tkey key, Tvalue value)
{
BinaryKeyValueNode<Tkey, Tvalue>
parent = null;
BinaryKeyValueNode<Tkey, Tvalue>
current = Root;
int compare = 0;
while (current != null)
{
parent = current;
compare =
current.Key.CompareTo(key);
current = compare < 0 ?
current.RightChild : current.LeftChild;
}
BinaryKeyValueNode<Tkey, Tvalue>
newNode = new BinaryKeyValueNode<Tkey,
Tvalue>(key, value);
if (parent != null)
if (compare < 0)
parent.RightChild = newNode;
else
parent.LeftChild = newNode;
else
Root = newNode;
newNode.Parent = parent;
Count++;
}
Reference current是我們嘗試插入和家長是當前子樹的父的子樹。只要當前指向的節點(第6行),我們不論向左或向右,根據當前節點的鍵和鍵,我們要在插入的值之間做比較。如果當前的key是我們要插入比右子樹的key更好,否則會到左側(10號線)。當我們已經達到了一個外部節點,Reference current將等於null。現在,我們建立了新節點並設置了所有正確的引用(線12-20)。
找到一個值,由於其主要的,工作方式非常相同,範例如下:
public Tvalue FindFirst(Tkey key)
{
return FindNode(key).Value;
}
public Tvalue FindFirstOrDefault(Tkey
key)
{
var node=FindNode(key, false);
return node == null ? default(Tvalue) : node.Value;
}
protected BinaryKeyValueNode<Tkey,
Tvalue> FindNode(Tkey key, bool ExceptionIfKeyNotFound = true)
{
BinaryKeyValueNode<Tkey, Tvalue>
current = Root;
while (current != null)
{
int compare =
current.Key.CompareTo(key);
if (compare == 0)
return current;
if (compare < 0)
current = current.RightChild;
else
current = current.LeftChild;
}
if (ExceptionIfKeyNotFound)
throw new KeyNotFoundException();
else
return null;
}
從root開始,我們比較這賦予key到當前節點的key。如果它們相等,就可以將其返回。如果這賦予key是完全地較大,我們繼續在右子樹的搜索,不然就在左側。接下來我們刪除操作:
protected void DeleteNode(BinaryKeyValueNode<Tkey,
Tvalue> node)
{
if (node == null)
throw new ArgumentNullException();
if (node.LeftChild != null && node.RightChild != null) //2 childs
{
BinaryKeyValueNode<Tkey, Tvalue>
replaceBy = random.NextDouble() > .5 ? InOrderSuccesor(node) :
InOrderPredecessor(node);
DeleteNode(replaceBy);
node.Value = replaceBy.Value;
node.Key = replaceBy.Key;
}
else //1 or less childs
{
var child = node.LeftChild == null ? node.RightChild :
node.LeftChild;
if (node.Parent.RightChild ==
node)
node.Parent.RightChild =
child;
else
node.Parent.LeftChild = child;
}
Count--;
}
protected BinaryKeyValueNode<Tkey,
Tvalue> InOrderSuccesor(BinaryKeyValueNode<Tkey, Tvalue> node)
{
BinaryKeyValueNode<Tkey, Tvalue>
succesor = node.RightChild;
while (succesor.LeftChild != null)
succesor = succesor.LeftChild;
return succesor;
}
protected BinaryKeyValueNode<Tkey,
Tvalue> InOrderPredecessor(BinaryKeyValueNode<Tkey, Tvalue> node)
{
BinaryKeyValueNode<Tkey, Tvalue>
succesor = node.LeftChild;
while (succesor.RightChild != null)
succesor = succesor.RightChild;
return succesor;
}
一個節點的缺失很容易造成,如果有零個或一個child。我們可以只連接parent和child ,忘了刪除節點(行12-18)。該BST屬性將仍持有。如果需要刪除節點有2名兒童,那麼我們就需要找到一個合適的節點來代替它由要么是在右子樹的最低鍵(按順序後繼)的節點,或者與節點在左子樹(在階前身)的最高鍵(行5-11)。我們決定哪一個有coinflip。
現在我們都必須在BST完成基本操作。假設要traversal整個樹狀結構,列舉的所有元素,其實有多種方法可以做到這一點,即depth-first或breadth-first。下面是執行所有3種方式進行depth-first traversal:
public IEnumerable<Tvalue>
TraverseTree(DepthFirstTraversalMethod method)
{
return TraverseNode(Root, method);
}
protected IEnumerable<Tvalue>
TraverseNode(BinaryKeyValueNode<Tkey, Tvalue> node,
DepthFirstTraversalMethod method)
{
IEnumerable<Tvalue> TraverseLeft =
node.LeftChild == null ? new Tvalue[0] :
TraverseNode(node.LeftChild, method),
TraverseRight = node.RightChild == null ? new Tvalue[0] :
TraverseNode(node.RightChild, method),
Self = new Tvalue[1] { node.Value };
switch(method)
{
case
DepthFirstTraversalMethod.PreOrder:
return Self.Concat(TraverseLeft).Concat(TraverseRight);
case
DepthFirstTraversalMethod.InOrder:
return
TraverseLeft.Concat(Self).Concat(TraverseRight);
case
DepthFirstTraversalMethod.PostOrder:
return
TraverseLeft.Concat(TraverseRight).Concat(Self);
default:
throw new ArgumentException();
}
}
public enum DepthFirstTraversalMethod
{
PreOrder,
InOrder,
PostOrder
}
上面的深度討論,是透過C#產生的一種子樹搜尋的演算。BST在資料結構中佔有很重要的地位,一些高級樹結構都是其的變種,例如AVL樹、紅黑樹等,因此理解BST對於後續樹結構的學習有很好的作用。同時利用BST可以進行排序,稱為二叉排序,也是很重要的一種思想。
-雲遊山水為知已逍遙一生而忘齡- 電腦神手
沒有留言:
張貼留言